재귀 란 ?
1. 어떠한 이벤트에서 자기 자신을 포함하고 다시 자기 자신을 사용하여 재정의하는 경우를 말한다.
2. 자가 증식의 종료를 명확하게 해야한다. (무한증식 오류)
1. 팩토리얼 (양의 정수를 순서대로 곱하는 순차 곱셈)
|
1
2
3
4
5
6
7
|
def factorial(n):
if n>0:
return n* factorial(n-1)
else:
return 1
print(factorial(5))
n이 0보다 크면 n-1 팩토리얼 값을 구하게 되며 0보다 작을 때까지 반복된다. n이 0보다 작으면 1이 리턴된다. |
cs |
-> math 모듈을 통해 math.factorial() 함수를 사용하여 간편히 구할 수 있다.
2. 유클레드 호제법 (x,y의 최대 공약수 , 큰 값을 작은 값으로 나누어 떨어질때까지 반복)
|
1
2
3
4
5
6
7
|
def gcd(x,y):
if y==0:
return x
else:
return gcd(y,x%y)
print(gcd(22,8))
|
cs |
-> math 모듈을 통해 math.gcd(a,b) 함수를 사용하여 간편히 구할 수 있다.
3. 피보나치 수열 구하기
1. for 문을 이용
|
1
2
3
4
5
6
7
8
|
def fib(n):
n1,n2=0,1
for i in range(n):
n1,n2=n2,n1+n2
return n1
print(fib(10))
|
cs |
2. 재귀함수를 이용
|
1
2
3
4
5
6
|
def fib(n):
if n<1:
return 0
if n<=2:
return 1
return fib(n-1)+fib(n-2)
|
cs |
1. 재귀 알고리즘 분석
|
1
2
3
4
5
6
7
|
def recur(n):
if n>0:
recur(n-1)
print(n)
recur(n-2)
recur(4)
|
cs |
- 하향식 분석 (위쪽에서 아래로 분석, 가장 왼쪽에 위치한 상자의 호출로 시작하여 계단식으로 조사해 나가는 방법)
recur(4)-> recur(3), print(4), recur(2) : 1 2 3 1,4,1,2
recur(3)-> recur(2), print(3), recur(1) : 1 2,3,1
recur(2)-> recur(1), print(2), recur(0) : 1,2,x
recur(1)-> recur(0), print(1), recur(-1) : x,1,x
-> 위에서 아래로 정리하면 1, 2, 3, 1, 4, 1, 2
- 상향식 분석 (아래쪽부터 쌓아 올리며 분석하는 방법)
recur(-1)-> x
recur(0) -> x
recur(1) -> recur(0), print(1), recur(-1) x,1,x
recur(2) -> recur(1), pirnt(2), recur(0) 1,2,x
...
-> 위에서 밑으로 정리하면 1, 2, 3, 1, 4, 1, 2
- 꼬리 재귀 제거하기
recur(n-2)를 n=n-2로 표현하고 다시 recur()함수를 호출하면 그 값은 같다.
def recur(n): if n>0: recur(n-1) print(n) recur(n-2) recur(4) |
def recur(n): while n>0: recur(n-1) print(n) n=n-2 recur(4) |
- 재귀를 제거하기
1. 제거하기 위해서는 n값을 임시로 저장할 공간이 필요
2. 함수를 처리하고 저장했던 값을 출력해야함
-> 스택으로 문제를 해결할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
from stack import FixedStack
def recur(n):
s=FixedStack(n)
while True:
if n>0: # n이 0이 될 때 if문은 더 이상 실행되지 않는다.
s.push(n) # 4,3,2,1 이 차례대로 s에 푸쉬된다.
n=n-1
continue
if not s.is_empty():
n=s.pop() # 팝 진행
print(n)
n=n-2 # 팝된 수에 -2를 하여 n이 2보다 클 때
continue # 푸쉬절로 들어가게 하여 다시 반복되게 한다. n
break # n이 0이면서 스택이 비어있을 때 종료
recur(4)
|
cs |
recur(4) 실행 -> if n>0 -> s.push -> 4번 반복 -> n=0
| n=0 | 4 | 3 | 2 | 1 |
if not s.is_empty() [ stk가 빌때까지 반복한다] -> 1출력-> n=1-2
| n= -1 | 4 | 3 | 2 | 1 |
-> 2출력 -> n=2-2
| n= 0 | 4 | 3 | 2 |
-> 3출력 -> n=3-2
| n= 1 | 4 | 3 |
-> if n>0 -> s.push -> 1번 반복 -> n=0
| n=0 | 4 | 1 |
-> 1출력 -> n=1-2
| n= -1 | 4 | 1 |
-> 4출력 -> n=4-2
| n=2 | 4 |
-> if n>0 -> s.push -> 2번 반복 -> n=0
| n=0 | 2 | 1 |
-> 1출력 -> n=1-1
| n= -1 | 2 | 1 |
-> 2출력 -> n=2-2
| n= 0 | 2 |
-> 비어있으므로 종료 출력 값: 1 2 3 1 4 1 2
* 하노이의 탑
n개의 원반이 있을 때 가장 밑에 있는 원반이 제일 크다.
1. 제일 밑에 있는 원반을 제외한 나머지 원반들이 보조 기둥으로 이동해야한다.
2. 제일 큰 원반이 목표 기둥으로 이동
1번 2번을 반복
1. 3개의 변수를 이용하여 하노이의 탑 구현 (원반 수, 출발 지점, 도착 지점)
|
1
2
3
4
5
6
7
8
9
10
|
def hanoi(n,start,end):
if n>1:
hanoi(n-1,start,6-start-end)
print(start,'->',end)
if n>1:
hanoi(n-1,6-start-end,end)
hanoi(3,1,3)
|
cs |
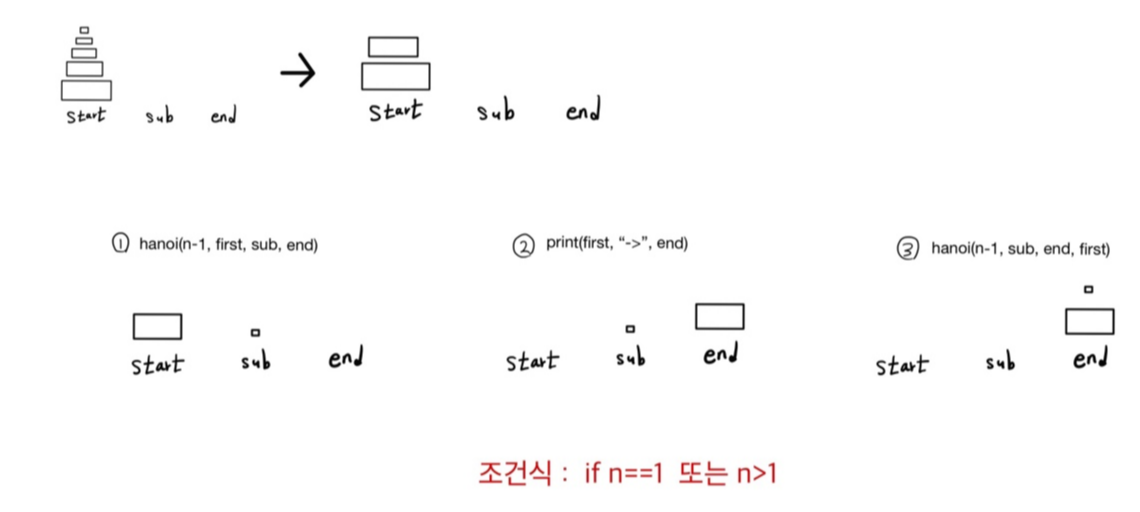
2. 4개의 변수를 이용하여 하노이의 탑 구현 (원반 수, 출발 지점, 도착 지점, 보조 지점)
|
1
2
3
4
5
6
7
8
9
10
11
|
def hanoi(n,first,end,sub):
if n==1: # 원반이 하나면 함수 종료
print(first, '->',end)
return
hanoi(n-1,first,sub,end) #
print(first,'->',end)
hanoi(n-1,sub,end,first)
hanoi(3,1,3,2)
|
cs |
* 어렵게 생각하지말기 ! 재귀를 단순화 시켜 원리를 파악하는 것이 중요하다.
* N 퀸 문제
퀸은 행/열, 대각선으로 어디로든 이동하여 상대를 공격할 수 있다.
그리하여 서로 공격하여 잡을 수 없도록 n개의 퀸을 배치한다.
- 8퀸 예제
- 모든 경우의 수 출력 (결과 : 16,777,216 의 경우의 수 )
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
pos=[0]*8
def put():
for i in range(8):
print(f'{pos[i]}',end=" ")
print()
def set(i):
for j in range(8):
pos[i]=j
if i==7:
put()
else:
set(i+1)
set(0)
|
cs |
- 행과 열, 대각선이 겹치지 않는 경우의 수
세로방향(행)에 하나씩 배치되게 설정
가로 방향 : j
/ 대각선의 경우 - j행 i열의 값은 i+j
\ 대각선의 경우 - j행 i열의 값은 i-j+7
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
pos=[0]*8
flag_a=[False]*8
flag_b=[False]*15
flag_c=[False]*15
def put():
for j in range(8):
for i in range(8):
print('■' if pos[i]==j else '□',end="")
print()
print()
def set(i):
for j in range(8):
if (not flag_a[j] and not flag_b[i+j] and not flag_c[i-j+7]):
pos[i]=j # i열 j행 대입
if i==7:
put()
else:
flag_a[j]=flag_b[i+j]=flag_c[i-j+7]=True
set(i+1)
flag_a[j]=flag_b[i+j]=flag_c[i-j+7]=False
set(0)
|
cs |
'Python > 자료구조 내용 정리' 카테고리의 다른 글
| 자료구조 7장 - 문자열 검색 (0) | 2021.08.26 |
|---|---|
| 자료구조 6장 - 정렬 알고리즘 (0) | 2021.08.13 |
| 자료구조 4장- 스택과 큐 (0) | 2021.08.02 |
| 자료구조 - 3장 검색 알고리즘 (0) | 2021.07.29 |
| 자료구조 - 2장 기본 자료구조와 배열 (0) | 2021.07.27 |
